Researchers and students must comprehend statistical learnability in machine learning. Strategic linear classifiers provide a basis for simulating decisions under manipulation. In practical systems, such as lending or hiring, participants often react strategically. Users alter input features to secure better outcomes when a scoring system is predictable. Statistical learnability shows whether classifiers can adapt to manipulated inputs.

The main question is whether the algorithm stays robust under manipulation. The walkthrough presents the proof in a clear and accessible way. This guide links theory to real-world uses. The importance of learnability in actual AI is also made clear to readers.

Understanding Strategic Linear Classifiers in Statistical Learnability

When data points are strategically adjusted to influence results, strategic linear classifiers are effective. When making predictions, these models record user behavior. Consider candidates altering their resumes to meet predetermined standards. The classifier must make predictions while taking these changes into account. Statistical learnability assesses how well the model adjusts in these situations. It shows how effectively the classifier maintains predictive consistency under manipulation.

Linear classifiers are preferred because their simple structure makes them easier to implement and analyze. They use a straight line in feature space to create a decision boundary. Shifts in strategic behavior characterize positions around this boundary. The accuracy of the predictions must be maintained while the model is updated. Learnability offers a framework for reliability testing. If the classifier is not learnable, it may not be able to handle frequent modifications.

Statistical Learnability Basics for Linear Classifiers in AI

The study of statistical learnability examines whether a learning rule produces a small prediction error. It evaluates how predictive accuracy changes with varying sample sizes. The goal of linear classifiers is to separate classes with the fewest possible errors. Learnability ensures the model remains consistent as training data grows. It takes into account both prediction bias and variance. Strategic behavior adds layers of difficulty to the analysis.

While maintaining boundaries, learners must adjust to changing features. Probability bounds are frequently used in learnability proofs. Classifier complexity is measured using concepts such as the VC dimension. The concept holds that simpler classifiers achieve stronger learnability. Generalization becomes more difficult as complexity increases. Deliberate adjustments by participants make the analysis harder to balance. In proofs, researchers try to strike a balance between accuracy and stability.

Key Proof Concepts in Statistical Learnability of Strategic Models

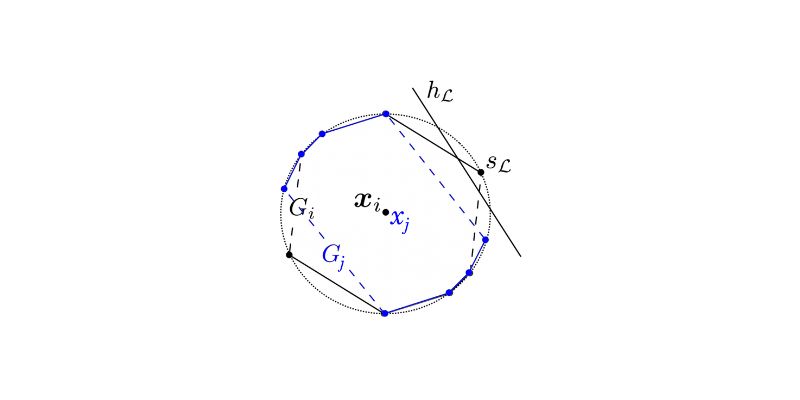
This analysis confirms classifier performance through mathematical techniques. First, the game setup is defined. As users modify inputs deliberately, the learner must adapt its predictions. Both the original and shifted probability distributions model data points. Mathematical reasoning shows that, under certain assumptions, error bounds remain small. A key stage in the analysis is ensuring convergence. It ensures that sample averages approach the expected values.

The robustness of linear decision boundaries against shifts is tested. Transformations on feature vectors are used to frame strategic behavior. The proof applies strategies from classical learnability to strategic contexts. Each assumption determines the complexity of the model updates. Key lemmas establish the connection between sample size and error rates. The conclusion demonstrates that strategic classifiers can be learned under specified rules.

Practical Examples of Strategic Learnability in Real-World Systems

Algorithms and agents often interact in applied settings. A clear case study of classifier manipulation is credit scoring. To increase their chances of getting credit, applicants can modify their reported incomes. Even with these changes, the classifier must make accurate predictions. Similar changes are made to resumes or applications on hiring platforms. When preparing for standardized tests, universities observe strategic behavior.

Despite manipulation, well-adapted models maintain equitable decision boundaries. Learnability guarantees the continued usefulness and consistency of these systems. By making frequent strategic adjustments, it stops unfair exploitation. The theory offers recommendations for creating robust prediction models. Real-world applications demonstrate the usefulness of mathematical guarantees in AI systems. Each example illustrates the importance of evidence-based learning frameworks. They relate theory to observable social results.

Challenges in Proof Walkthrough of Learnability for Strategic Classifiers

Students frequently find the proof technically demanding. Standard learning boundaries are disrupted by intentional feature adjustments. Students need to keep a close eye on distribution changes. Each shifted feature vector alters the classification results. Managing distributional stability under transformations is difficult. Bounding classifier error rates present another difficulty. The proof must confirm broader applicability even under manipulation.

Strategic behavior necessitates adjustments for complexity measures such as the VC dimension. The mathematical notation can often be confusing at first glance. Researchers often handle complexity by relying on simpler assumptions. Yet, these assumptions may limit the practical applicability of the proof. For researchers, striking a balance between rigor and practicality remains a challenge. Proof walkthroughs use sequential logic to simplify each section. The method gives beginners in learning theory greater confidence.

Future Directions for Statistical Learnability in Strategic Classifiers

Stronger models for strategic environments are investigated in future studies. Nonlinear classifiers might be better at handling manipulation. Neural networks could adjust decision boundaries in response to changing data. For more complex settings, researchers test deeper proofs. Analysis is improved when statistical learning and game theory are combined. Real-time updates against manipulation are possible with adaptive algorithms.

Regulators may demand fairness checks in strategic systems. Fairness constraints for robustness could be incorporated into learnability proofs. Stability and minimal computation are necessary for practical systems. In the real world, theories must adapt to vast amounts of data. Researchers use user behavior simulations to test proofs. A key component of responsible AI design is still learnability. Accuracy and resilience must continue to be balanced in future models. Collaboration between the theory and application communities is necessary for progress.

Conclusion

The statistical learnability of strategic linear classifiers bridges the gap between demanding mathematics and real-world AI requirements. Strategic environments also reflect practical challenges found in everyday applications. Classifiers that adapt under manipulation prove to be more stable. The framework provides assurances that forecasts remain accurate and reliable. Practical applications highlight the influence of theory on everyday systems. Future research promises scalable, equitable, and adaptable solutions. Learnability provides a foundation for developing reliable AI applications. The proof walkthrough guarantees easy access to a complex topic. Readers depart with curiosity and clarity. The way forward blends responsibility and reason.